15900번: 나무 탈출
평소에 사이가 좋지 않던 성원이와 형석이가 드디어 제대로 한 판 붙으려고 한다. 성원이와 형석이 둘과 모두 똑같이 친한 인섭이가 대결 종목을 정해 가져왔다. 바로 '나무 탈출' 이라는 보드게
www.acmicpc.net
1. 풀이방법
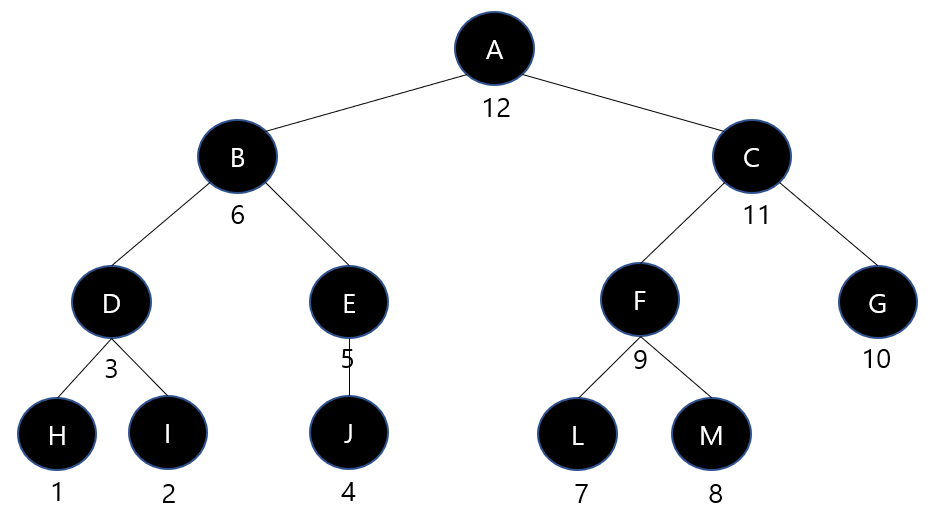
- 트리 구조를 이용한 DFS문제 입니다.
- 처음에 문제를 읽으면서 가장 고민이 되었던 건 리프노드는 구별이 가능한데 (간선이 1개뿐인 놈(루트제외))
- 리프노드에서 한칸 타고 부모로 올라갔을 때, 그다음 부모노드가 어떤 녀석인지를 판정을 어떻게 해야하나
- 고민을 많이하고, 결국 class로 노드를 만들어 포인터를 통해서 인접리스트 방식으로 트리를 구현해야하나 생각
- 했었는데, 너무 하기 귀찮아서 다시 문제를 읽어보았는데
- 사실 문제가 원하는 출력이 그렇게 복잡하지 않습니다. 이기냐, 지냐 만 출력하는 문제이므로
- 사실 각각의 리프노드들로 부터 루트노트(1) 까지 가는 간선의 수 (즉 높이) 들의 합이
- 홀수이냐, 아니면 짝수 이냐만 파악하면 문제의 정답을 출력할 수 있었습니다.
- 즉 ! 높이만 알면 되므로 리프노드 부터 탐색할 필요가 없이, 루트노드부터 dfs를 통해 리프노드까지 가면 됩니다!!!!
- 가장 고민하던 문제가 해결되었습니다. 그 다음 부터는 쉽습니다
- 그러므로 vector<int> tree[500001]을 통해 트리의 간선정보를 담고
- bool visitnode[500001] 을통해 위에서 내려오는 부모노드는 방문체크를 하여 dfs탐색에서 제외 시켜줍니다.
2. 주의사항
- 리프노드는 연결된 간선이 무조건 하나!!!! 하지만 여기서 주의할 것은 간선이 하나가 될 수 있는 녀석이 하나 더
- 있습니다..>! 바로 루트노드는 간선이 하나만 연결될 수 있습니다. 그러므로 종료조건에 s!=1(루트노드)를 추가
- 해주었습니다.
3. 나의코드
#include<bits/stdc++.h>
using namespace std;
int N;
vector<int> tree[500001]; // 메모리때문에 인접행렬은 x
bool visitnode[500001];
int totalheight = 0;
//간선이 하나만 존재하면 리프노드
void dfs(int s, int cnt) {
if (tree[s].size() == 1 && s!=1) { //리프노드
totalheight += cnt;
return;
}
for (int i = 0; i < tree[s].size(); i++) {
if (!visitnode[tree[s][i]]) {
visitnode[tree[s][i]] = true;
dfs(tree[s][i], cnt + 1);
visitnode[tree[s][i]] = false;
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> N;
for (int i = 0; i < N - 1; i++) {
int tmp1, tmp2;
cin >> tmp1 >> tmp2;
tree[tmp1].push_back(tmp2);
tree[tmp2].push_back(tmp1);
}
visitnode[1] = true;
dfs(1, 0);
if (totalheight % 2 == 1) cout << "Yes" << "\n";
else { cout << "No" << "\n"; }
return 0;
}'알고리즘 문제풀이 > DFS와 BFS' 카테고리의 다른 글
| 백준 2638 [C++] (0) | 2021.01.24 |
|---|---|
| 백준 2251 [C++] (0) | 2021.01.19 |
| 백준 1600 [C++] (0) | 2021.01.19 |
| 백준 12851 [C++] (0) | 2021.01.18 |
| 백준 13913 [C++] (0) | 2021.01.18 |