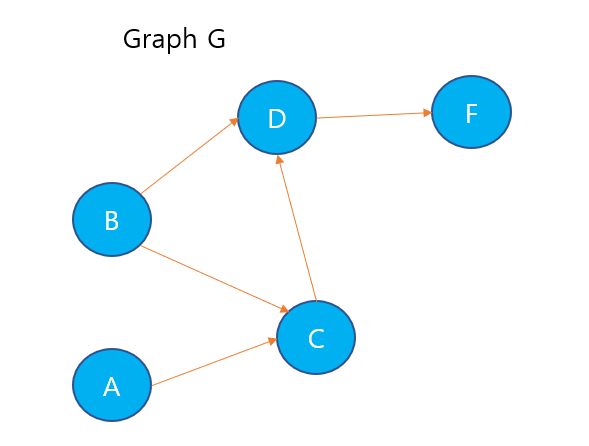
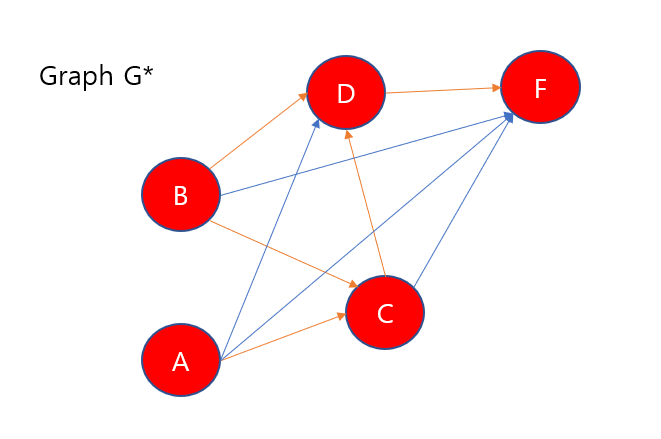
0.Transitive Closure
- 그래프 G가 주어졌을 떄 G*은 G와 같은 정점집합(same vertices)을 가진다.
- 만약 그래프 G가 정점 u에서 v로 경로를 가지면 그래프 G*는 정점 u에서 v로 간선(edge)를 가진다.
- Transitive Closure은 경로가 존재하는 지 여부를 알 수 있다.
- 물론 모든 정점에서 DFS를 수행하면 O(n(n+m)) --링크드리스트로 구현되어있다면
에 알아낼 수 있다.
1. 개요
- 플로이드 워셜 알고리즘은 그래프에서 Transitive Closure을 구하거나
n:n(다대다) shortest path를 구하는 데 사용 된다.
- Dynamic Programming 알고리즘이다.
- "A에서 B로 갈 수 있고 B에서 C로 갈 수 있는데 AC간선이 없다면, 간선을 연결해준다."
2.아이디어
- 모든 정점들을 번호로 관리한다.
- n단계로 구성되어 차례차례 확장해나가는 구조.
- k번째 단계의 수행이 완료되면, 1~k까지의 간선들은 모두 활용한 것 이다.
- 친구들끼리 연락을 해야하는 상황을 생각해보면 이해가 쉽다.
(난 A의 전화번호를 모르지만 B의 번호를 알고있다. B는C의 번호를알고있다.
그럼 난 두 단계를 거치면 C의 번호를 알게된다.)
3.The Floyd-Warshall Algorithm(플로이드 워셜 알고리즘)
- 각 단계의 그래프를 G0,G1,.......Gn이라 하자.
- 정점들은 v1,v2,.....,vn이라 한다.
- k단계에서 Gk는 Gk-1으로 부터 계산한다.
- 수행시에 adjacent연산을 많이 쓰는데 (두 정점 사이에 경로가 있는지 u->v)
그럼 Graph를 구현 할 때 인접행렬로 구현하는 게 좋겠죠~
- 전화번호 예시에 빗대어 설명하였습니다.

-그럼 n:n shortes path는 어떻게 구하느냐??
- 기본적인 원리는 위와 같습니다만, 새로 알게된 경로가 기존의 경로보다 짧을 경우에 그 값을 넣어주고
그렇지 않은 경우는 update하지 않습니다.
- 처음 초기화를 무한대로 해줍니다.

4.Example
(1)

(2)

(3)
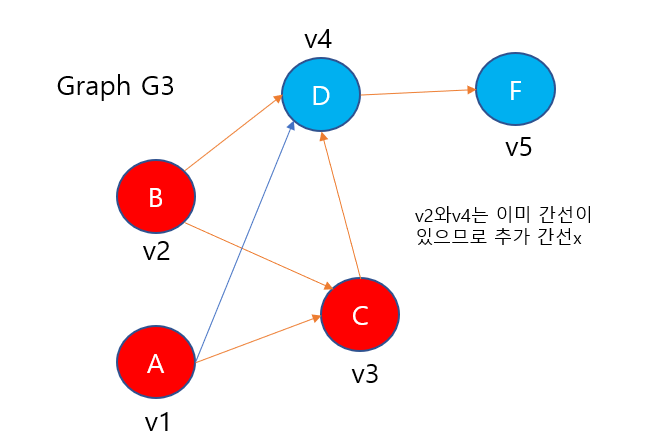
(4)

(5)

5. 분석(Analysis)
- n:n shortest path를 구할 때 n번의 다익스트라 알고리즘을 호출하면 O(nmlogn)의 시간 복잡도를 가진다.
- 플로이드 워셜 알고리즘은 O(n*3)의 시간 복잡도를 가진다.
'알고리즘 > 최단거리(shortest path)' 카테고리의 다른 글
| Dijkstra's Algorithm(다익스트라 알고리즘) (0) | 2020.10.11 |
|---|