Dijkstra's Algorithm(다익스트라 알고리즘)

0. 시작에 앞서...

- 만약, 그래프가 가중치가 모두 같은 간선들로 이루어져 있다면 BFS(넓이 우선탐색)을 통하여 쉽게

   최단거리를 구할 수 있다.

- 오늘은 가장 유명한 최단거리 구하는 알고리즘인 다익스트라 알고리즘에 대하여 알아보겠다.

 

 

1. Shortest-Path 정의

- 그래프 G=(V,E,W)에서 P는 nonempty-path이라 하자

- W(P) (Weight of P) = the sum of the weights (각 간선들의 가중치의 합)  이다.

- 만약 x=y (즉 같은 정점) 사이의 가중치는 0 이다.

- x정점과 y정점사이에 W(P)보다 가중치가 작은 path가 없다면 이 경로가

    shortest-path or minimum-weight path이다

 

 

2.Properties of Shortest Paths

- Lemma: shortest path property

- 간단하게 말하면 최단경로는 최단경로들로 구성되어있다 라는 것.

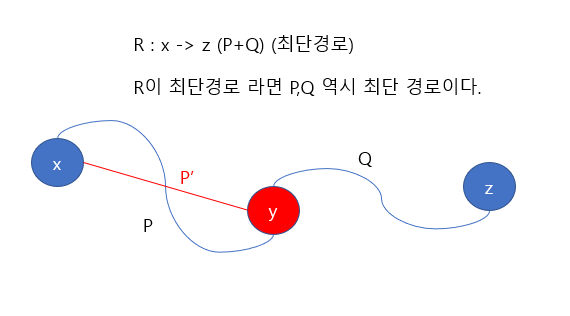
- 이는 귀류법으로 손쉽게 증명할 수 있다.

- if) P가 최단경로가 아니거나 Q가 최단경로가 아니라면(즉, 위 그림처럼 P'가 존재)

           W(P')<W(P)이고 W(P')+W(Q)<W(P)+W(Q) 즉 R이 최단경로가 아니다.

 

3. Dijkstra's Algorithm(다익스트라 알고리즘)

- Weight are nonnegative (가중치는 음수가 아니여야한다.)

- greedy 알고리즘 이기도 하며 dynamic programming 알고리즘 이기도 하다.

- 기본적인 구조는 prim 알고리즘과 비슷하다.

 

 

4.Example

- 가중치가 같다면 알파벳 순서로 선택한다고 가정.

(1) A-출발점

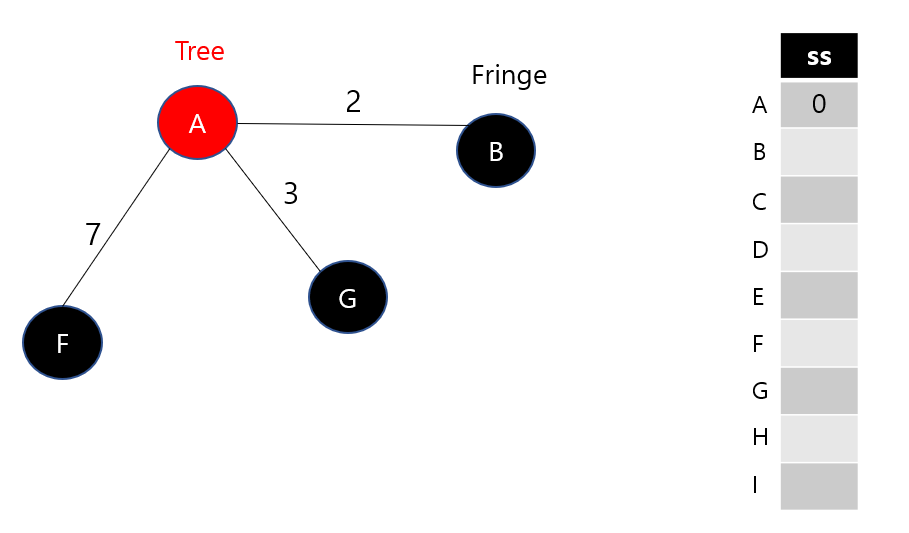
(2) 가중치가 가장 짧은 간선 2를 선택 결과 테이블 UPDATE

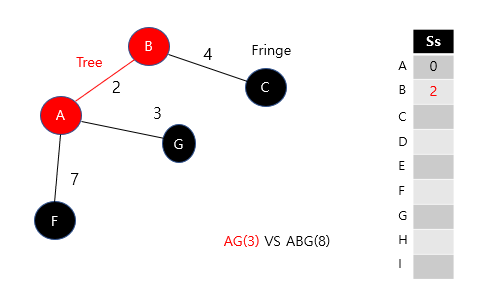
(3) AG(3)을 선택

(4) BC(4)를 선택

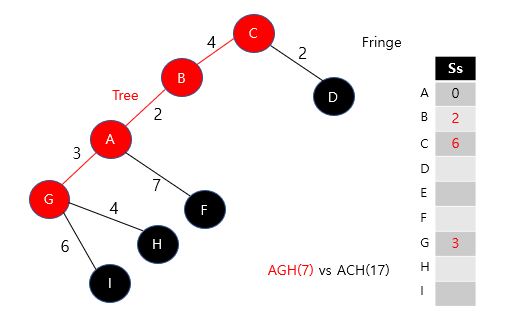
(.....) 이런식으로 테이블을 업데이트 해서 끝나면 A점으로 부터 다른 정점들로의

최단거리를 테이블에서 불러오기만 하면 된다.

 

 

5.Correctness

- 새로운 경로가 나타날 수 도 있는데 최단경로를 이렇게 확정해버려도 되는가?

- 간선의 가중치는 음수가 아니므로 새로운 경로가 나타도 같을 순 있어도, 

   더 짧은 경로가 나타날 순 없다.

 

6.분석(Analysis)

- 힙자료구조를 이용한 우선순위 큐 사용시 시간복잡도는 O(mlogm) = O(mlogn)

이라 할 수 있습니다.