대엉코딩

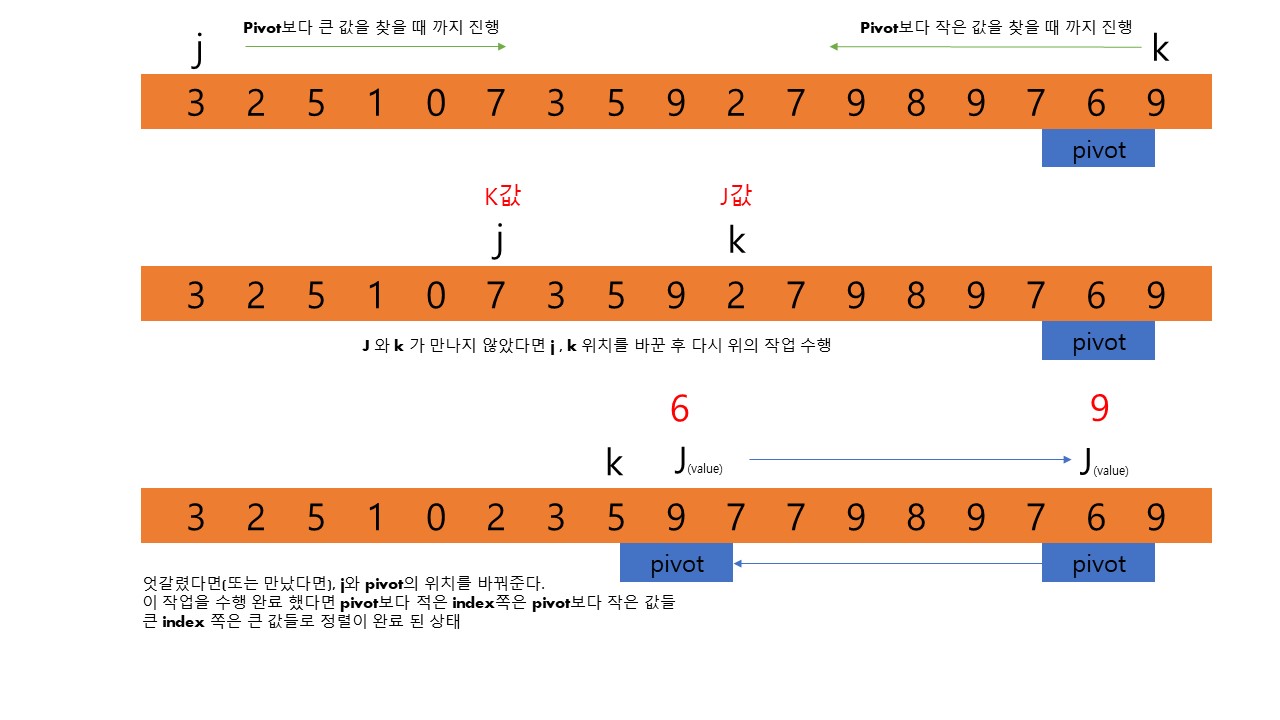
1. 기본 개념

 - 만약 순서대로 정렬된 두개의 배열 이 있다고 생각해보자.

 - 이 두 배열을 합쳐서 정렬된 배열을 얻고자 할때는 첫번째 elemet끼리의 비교만을 반복하면 된다.

    (둘 중 하나의 배열이 끝날때 까지만)  ---> 즉 가장 많이 비교할때는 (지그재그) n-1, 적게는 n/2 이다.

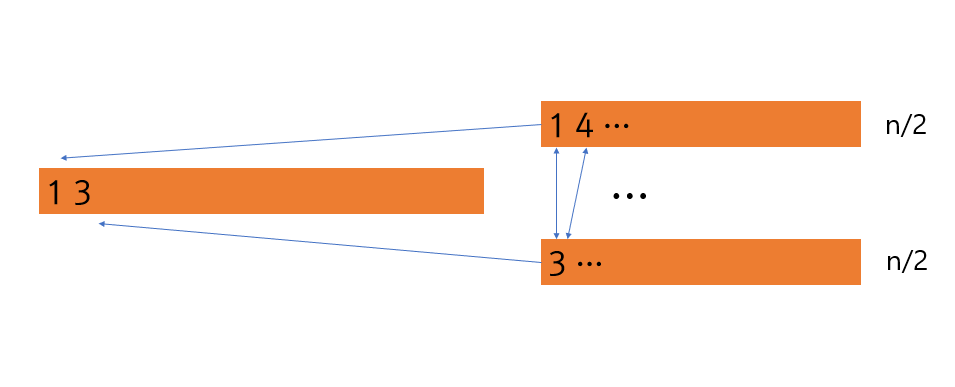
//지금 까지 설명한 것이 병합(merge) 과정이다.

2. mergesort의 대표적인 특징 

 - divide and conquer 전략을 이용하는 대표적인 알고리즘이다.

 - 원소들 끼리 대소를 비교해서 정렬하는 알고리즘 중에서는 최적의 알고리즘 이다.(O(nlogn))

3. MergeSort Strategy

 - 입력받은 배열을 divide 한 후 merge 한다. 

 - (merge를 하는 과정에서의 아이디어는 1에서 설명한 내용과 같다.)

 - 모두 merge를 하면 sort가 완료된 상태이다.

 - divide를 완료한 상태에서 sort를 진행하면서 Merge 하면서 올라오므로 merge가 완료 됬다면 sorted 된 상태이다.

4. Algorithm : Mergesort

5. Analysis

 위의 의사 코드를 확인 하고 분석해보면 이러한 점화식이 나온다.

 W(n) =O(1)+O(1)+W(n/2)+W(n/2)+Wmerge(n)

 (by MasterTheorem)

 =====>>> Θ(nlogn)

6. 구현

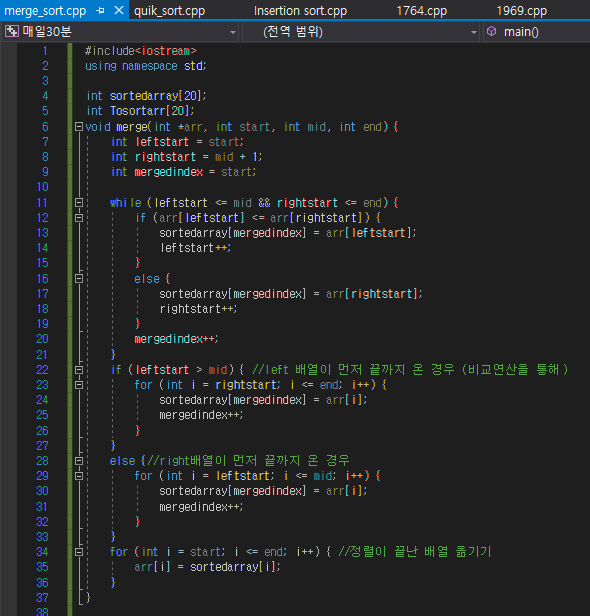
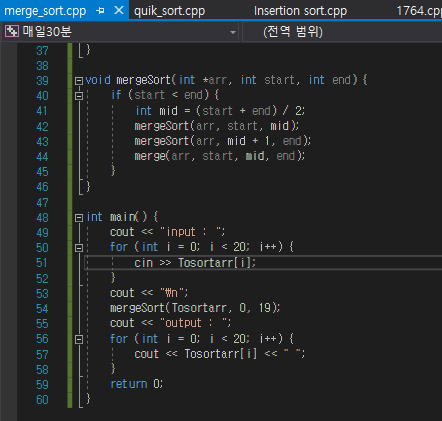
결과화면

** divide and conquer(분할 정복) 은 알고 들어가야한다. --> 퀵소트가 사용하는 기법

1.Quick-sort

 - random 한 속성을 가진 형태의 input을 정렬하는 데 성능이 매우 좋다.

 - pivot 이라는 하나의 element를 기준으로  L(less), E(equal), G(greater)로 나눈다 (분할)

 - 나눈후  L 과 G(E U G) 로 다시 recursive하게 sort를 수행한다.

2. Worst Case

 - 최악의 경우 pivot을 잡고 분류를 하는 과정에서 L,G를 나누는데 계속 한쪽으로 몰리는 경우 이다

 - 이럴경우 n-1번을 나누게 되고 (depth = n), 각 단계에서 약 n, n-1, n-2 ....... 1까지 진행되므로

 - running  time의 합은 n+(n-1)+ ... +1 이므로 최악의 경우 O(n^2) 이다.

3. Average Case

 - 평균분석의 경우 O(n*logn) 이다.

 - 최악의 경우는 느리지만 평균분석은 상당히 빠르다.

4. 알고리즘

-partion 별 

5. 특징

 - partion을 한번 하면 pivot은 자신의 위치를 찾는데 그 자리가 최종 출력 위치이다.

 - in-place 로 구현 가능 (추가적으로 사용하는 메모리가 tmp변수 하나 정도로 O(1) 정도

6. 구현