대엉코딩

0. 프로그램이란?

 - "실행할 수 있는 파일 ( 무언가 작업하기 위해 ) "

 - ex) 윈도우의 exe 파일 

1. 프로세스 란?

 - " 실행되고 있는 컴퓨터 프로그램 (독립적) "

 - 각 프로세스는 각각의 자원을 할당 받는다.

 - 프로세스 간의 통신 위해서는 파이프, 소켓등을 사용해 통신한다. (비용이 상대적으로 많이 든다.)

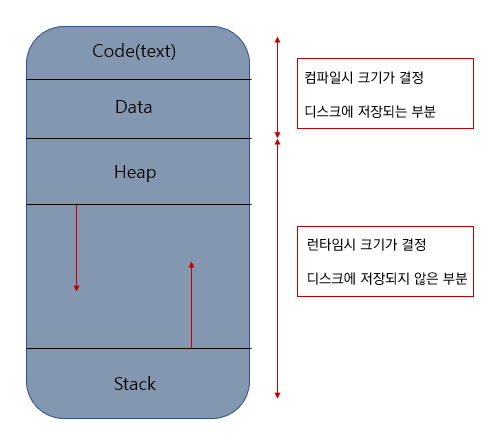
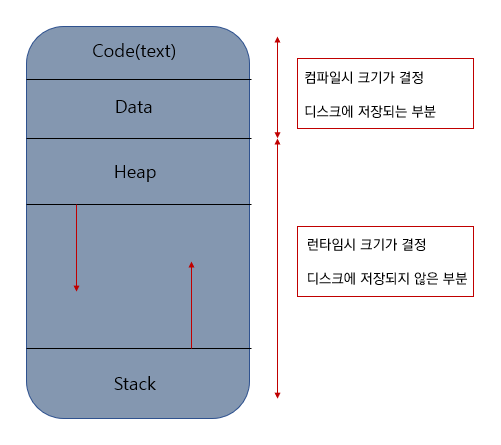
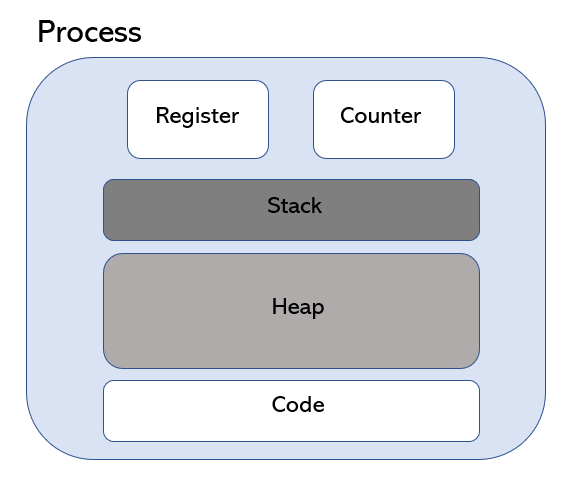
 - Register, Counter, Stack, Heap, Code 으로 구성된다

 - 시작, 종료, 컨텍스트 스위칭 시 비용(시간) 이 많이 소요된다.

 - 프로세스 간의 전환에는 운영체제 호출을 필요로한다.

1-1. 프로세스 제어 블록(PCB) 란?

- 운영체제의 자료구조

- 프로세스에 정보를 저장하고 있다.

- 운영체제는 프로세스 생성과 함께 PCB를 생성한다.

- 프로세스 스위치가 발생하면 진행중이던 작업들은 PCB에 저장하고 CPU를 반환한다.

- 다시 CPU를 할당받으면 PCB에서 복원해와 종료시점부터 다시 작업을 수행한다.

- 프로세스 ID, 프로세스 상태, 프로그램 카운트(다음 실행 명령어의 주소), CPU레지스터 등이 저장된다.

2. 쓰레드 란?

 - " 프로세스의 하나의 실행 단위 "

 - 프로세스 안에서 각각의 작업을 처리한다.

 - 프로세스 안에서 동시성(concurrency)을 가지고 진행한다.

 - 한 프로세스 안의 여러개의 프로세스들은 Code, Data, Heap은 공유하고, 각각의 Stack을 가진다. 

 - 시작, 종료, 컨텍스트 스위칭 시 비용(시간) 이 적게 소요된다.

 - 쓰레드 간의 전환에는 운영체제를 호출할 필요가 없다.

 - 자원을 공유하는 만큼, 공유자원에 접근하고, 변경을 할 때 주의가 필요하다.

2-2. 멀티스레딩 이란?

- 하나의 프로세스를 다수의 실행 단위로 구분하여 자원을 공유하고 자원의 생성과 관리의 중복성을 최소화하여 성능을 향상시키는 기법

- 각각의 스레드는 각각의 스택과 PC레지스터 값을 가진다.

- 독립적 실행흐름을 위해서 스택은 필요하다. (각각 가지는 이유)

- 스레드는 하나의 실행 단위 이므로 PC레지스터를 통해 실행위치를 CPU할당에 따라 저장,복구하여 그 위치에서 다시 실행한다.

1. 힙 메모리를 사용하는 이유?

- 위의 그림에서 보듯이 heap의 공간과 stack 의 공간에 나누어져 있습니다.

- 그리고 stack메모리의 경우 사용되는 양은 런타임시 결정이 되지만 스택메모리의 최대 공간 (사용가능한) 은 컴파일 시

  이미 지정이 됩니다.

- 왜 스택공간이 있는데 굳이 힙 메모리를 사용해야 하는가 ? 에 대한 궁금증이 떠오르게 됩니다.

- 제가 경험해보고 아는 선에서 몇가지만 이야기해보겠습니다.

-- (1) dynamic (동적할당)

         알고리즘 문제를 풀 때 처럼 입력의 최대값이 정해져 있는경우 그 최대치로 메모리 공간을 할당해서 컴파일 시간

         에 결정을 해서 스택메모리를 사용할 수도 있지만 (큰 사이즈의 경우 다음에 언급), 만약 사용자에 입력에 의해서 

         공간의 변동이 정해지는 경우 개발자 입장에서 미리 그 크기를 예측할 수 없으므로 런타임 시간에 변동에 맞게 

         메모리를 할당해야하는 경우 입니다.

-- (2) size 문제 (엄청 큰)

         이전 게시글에서 언급했다싶이 stack memory의 경우 최대 사이즈가 미리 정해지는 만큼 엄청 큰 사이즈가 필요

         할 경우 stack overflow가 발생할 수 있습니다. 이 때 스택에는 주소를 가리키는 포인터만 설정해주고, heap 메모

         리 공간에 큰 사이즈를 선언해서 가리키게끔 할 수 있습니다.

-- (3) 스택메모리의 life cycle

         스택 메모리의 경우 stack frame단위로 쌓이게 되는데 그 함수가 끝날경우 (life cycle)이 끝날 경우, 스택 메모리에

         서 해제됩니다. 이 경우에도 어떤 데이터를 유지하고 싶을 때는 힙 메모리 공간을 사용합니다. (직접 해제 해주기 

         전 까지 힙 영역에 저장하고 있는 데이터는 사라지지 않으므로)

2. 힙 메모리 사용 in C++

- stack 메모리 대신 heap 메모리를 사용하는 경우는 필요한 용량이 매우 크다던지, dynamic(동적)으로 런타임 시간에

   결정이 되는 변수를 사용한다던지 할 때인데요

- C++에서는 new를 통해서 힙에 공간을 할당 받고 스택 메모리에서의 포인터 변수가 이를 가리키도록 합니다.

- new를 통해서 할당을 받을경우 반드시 까먹지말고 delete을 해주어야만 메모리 leak을 막을 수 있습니다.

- new이외에도 unique_ptr 을 사용한다던지, 배열의 경우 vector를 사용하여 힙에 선언을 해준다면

- 메모리 해제 과정을 신경쓰지 않아도 되게끔 좀 더 안전하게 사용하실 수도 있습니다. 하지만 new를 사용하신다면

- 까먹지말고 반드시 delete으로 해제를 해주어야 한다는 점.!

3. stack 메모리 사용할 때와 heap 메모리 사용할 때의 차이점(장단점?)

- 우선 stack에 선언할 경우 속도가 더 빠릅니다.

- heap의 경우 원하는 만큼의 공간의 힙메모리상에서 찾고 할당하고 나중에는 이를 해제해야 하므로 상대적으로 시간이

- 많이 소요됩니다.

- 그럼에도 heap에는 큰 용량을 필요로 하는 변수라던지, 동적으로 결정이 되는 변수일 때 사용이 가능합니다.

- 그러므로 큰 사이즈가 아닌 경우 (100kb 미만? 정도?) 정도는 속도가 빠른 스택메모리를 사용하는 것이 좋습니다.

- 또 다른 차이점은 스택메모리의 경우 여러번수를 선언하고 주소를 찍어보시면 아시겠지만,

- 빽빽하게?? a가 4바이트를 차지하고, b가 4바이트를 차지한다면 메모리 주소도 4바이트(32bits) 차이가 납니다.

                   (물론 연속되게 위치하고 있을 경우를 가정)

- 중간에 빈 공간없이 빽빽하게 차지하지만, 힙의 경우 구멍이 송송뚤린 것 처럼 사이에 공간이 있습니다.

- 스택처럼 빡빡하게 메모리를 채우지는 않습니다.

0. 메모리 구조를 알아야 하는 이유.

- c++는 개발자가 메모리를 관리를 할 줄 알아야하고, memory 누출이 발생할 경우 (만약 지속적으로)

프로그램이 오류가 날 수도, 다운이 될 수도 있습니다.

- 컴퓨터 구조론인가.....배울 때 많이 학습했던 부분인 것 같은데 시간이 꽤 경과되어서... 다시 중요한 부분 위주로 다시 정리해보겠습

   니다.

1.  메모리 구성

2. Stack

- 이번 글에서는 c++의 스택구조에 대해서 상세히 정리를 해볼까 합니다.

- 변수의 코드를 짜서 포인터를 이용해서 주소를 출력해보시면 아시겠지만, 변수의 주소가 스택으로써 아래에서 위 저장

- 컴퓨터는 변수의 이름을 저장해서 바로 접근하는 것이 아닌, stack의 top의 위치에서 얼마나 떨어져있는지를 기억하여 

  접근합니다.

3. 스택프레임

- 사실 Stack 메모리에 쌓이는 단위는 변수 단위가 아닌 스택프레임 단위인데 이는 function단위 입니다.

- 변수가 하나씩 쌓이는게 아니라 function에서 차지하는 메모리 만큼이 한번에 stack에 쌓이는 것입니다.

- 또한, stack에는 function이나 main 함수의 변수들 뿐만 아니라 스택에 쌓인 function이 종료되면 다시 그 이전의

- 함수 (메인이 될수도, 또다른 function이 될수도)로 돌아 가야 하기 때문에 function call을 한 function 의 return     

   address , 그리고 그 function의 arguments 등이 같이 스택메모리 공간에 쌓입니다.

- 그 function이 끝나면 스택메모리에서 해당부분이 사라집니다.

- 프로그램 실행시 어느정도의 메모리 공간을 확보하는데 간단한 예로 너무 깊이 재귀함수를 실행할 경우, 이 스택메모

  리 공간에 계속 쌓이게 되고, 이는 스택오버플로우를 발생시키는 경우를 종종 확인하실 수 있습니다.

- c++에서는 this라는 키워드를 제공하는데 , 이를 통해서 함수를 실행하면서 객체의 멤버 변수에 쉽게 접근할 수 있습니

  다. this 역시 스택프레임에 객체의 주소를 가지고 올라감으로써 쉽게 객체의 멤버변수에 접근할 수 있도록 해주고 있

  습니다.

1. constuct Heap

 - heap sort를 위해서는 일단 입력으로 들어온 배열을 heap의 조건을 만족 하도록 만들어 줘야한다. (구조,순서)

 - 중요한 것이 있는데 heap의 구조조건은 full binary tree 이기 때문에 사실 입력(배열) 자체가 구조조건을

   만족한다.

 - 그럼 우리는 순서 조건만 맞춰서 힙을 구성하면 된다 ! 어떻게 할 것인가? 

 -밑에 자식쪽의 서브트리는 heap조건을 만족 할 때 위와 같이 하나의 노드를 삽입하면

 -순서조건이 check 되지 않은 노드는 단 하나뿐이다. --> 이 노드에 대해서 fixheap을 수행 하면

 n+1짜리의 heap이 완성 된다. (이 과정은 O(logn) -->하나의 원소를 heap에 삽입하는))

 - 이 아이디어로 밑에서부터 heap을 구성해 나가는 것이다.

2. Analysis

 - 이제 힙을 구성하고 sort 하는 것 까지 알아보았다 .... 성능 분석을 해보자 !

 - 먼저 heap construction 부분에서 짚어보자.

- 언제가 최악의 경우? (Worst case) ---> construct힙을 하는데 계속 그 노드의 위치가 leaf노드 일 때 이다

  (끝까지 내려갈 때) 

- 각 노드가 삽입 될 때 (heap을 구성하기 위해) 자신의 자리를 찾아 갈 때 규칙을 한번은 오른쪽으로 내려가고

   그 이후에는 쭉 왼쪽으로 내려간다고 하자.

 - 저렇게 내려갈 경우 힙을 다 구성 했을 때 leaf노드로 내려간 간선이 겹쳐지는 일이 없다 !

    (서로 다른색이 지나갈 때 지나간 간선을 다른 노드가 지나갈 때 그 간선을 지나가는 일이 없다)

 - construct heap 과정에서 하는 총 비교연산의 수 <= 2(비교연산) * n-1(간선의 수) ---> O(n)

 - heap sort의 최악의 경우 --->  O(2nlogn)  (sort)   +   O(n) (힙 구성)  -->  O(nlogn) 이다

 - 대소비교 연산을 이용한 sorting의 경우 O(nlogn)보다 빠를 수는 없으므로 optimal 이라고 할 수 있다.

3. Accelerate Heapsort (BubbleUpHeap)

-- > heap sorting  과정에서 fixheap을 할 때 각 단계에서 노드는 두번의 비교연산을 수행했었다.

      ( 둘 중의 누가 더 큰 자식인가 )  +  (본인과 더 큰 자식과의 비교)

- 이렇게 매번 내려갈 때 마다 두번의 비교연산을 하지 말고 한번 (둘 중의 누가 더 큰 자식인가)

   만 비교하고 무조건 그 큰 자식 쪽으로 내려간다 ( 언제까지? h/2 즉 절반정도 내려올 때 까지 )

- h/2 정도 까지 내려왔을 때 부모 노드와 비교연산을 한번 실시한다..!

- 1) 부모노드가 더 크다면? (조건만족) -->다시 나머지 h/2에 대해서 recursive 하게 다시 수행

      --> 다음엔 h/4만큼 가고 다시 비교하고...또 reculsive....!

  2) 부모노드가 작다?? --> 너무 많이 내려왔다....비교를 통해 다시 위로 올라가 내 자리를 찾아간다.

3-1 Accelerate Heapsort Analysis

 - 연산의 수를 살펴보자 (최악의 경우)

 - h/2 (이만큼 한번의 연산을 통해 내려온다) + 1(부모노드와 비교) + h/4 (다시 진행) +1 ......

   <= h (h/2+h/4+.......) + logh (1+1+...... --->log 높이)  라고 할 수 있겠다 

 - h= logn 이다 즉 . 이 방법을 통해 서 우리는

 - worst case가 nlogn+Θ(nloglogn) 임을 알 수 있다.

 -점근 분석을 하면 최악의 경우는 앞에서 본 힙소트(O(2nlogn)) 과 O(nlogn+nloglogn) 모두 O(nlogn) 이지만

 - 비교 연산의 수는 절반 정도 줄여서 성능을 향상 시킬수 있다고 생각할 수 있다.

0. heap?

 - 구조 조건과 순서 조건을 가지고 있는 자료구조 이다.

 - 구조 조건 : 이진트리인데 갚이가 h 일 때 h-1까지는 full binary tree 이고 h번째에는 왼쪽부터 차례대로 채운다.

 - 순서 조건 : 부모노드는 자식노드 보다 크다 (max-heap 일 때) , 직계가 아닌 노드 끼리는 상관이 없다.

1. heap sort?

 - 위에서 언급한 heap 이라는 자료구조를 이용한 sort 방법이다.

 - heap의 특성을 생각 한다면 ? n개의 정보를 sort하기 위해선

 - data를 heap 구조로 construct 하면 root 노드 에 있는 값이 가장 큰 값이므로 그 값을 빼오면 된다. 

    (n번의 삭제연산을 수행 하면 sort가 완료된다.)

2. delete(root) and fixheap ? (downheap)

 - 루트에 있는 노드(제일 큰값을) 가져갔다고 하자. 그러면 남은 노드들로 다시 heap을 만족하도록

   트리를 구성해야 그 다음 루트노드를 또 삭제할 수 있다 (두 번째로 큰값이겠죠? 전체에서? )

 - 그렇다면 생각 해보자 ..... 루트를 제외하고 남은 트리에서 heap이 되게 하려면

 - 구조 조건과 순서 조건을 만족해야 하는데...... 어떤 것을 만족하는게 더 쉬울까 ? ----> (구조조건?)

 - 왜?? 만약에 n-1개의 노드가 남아 있다고 할때 heap의 구조조건을 만족하도록 만드는 모양은 하나뿐이다.

    ( 즉 위치로 보자면 어디 위치의 노드가 없어지느냐 ? 맨 밑 리프 노드 열에서 가장 오른쪽의 노드 !)

    ( 이 위치는 O(1) 에 바로 찾을 수 있다...! ....왜? heap은 배열로 구현 하기 때문에 맨 마지막 index의 노드!)

 - 그럼 일단 가장 오른쪽에 위치한 리프노드를 루트 노드로 덮어 쓰자 ! --->구조 조건은 만족 !

 - 이제 순서조건을 생각해보자 .... 일단 루트노드로 덮어쓴 가장 오른쪽 리프 노드가 다시 자신의 자리를 

 - 찾아갈 수 있도로 해야 하는데 이 과정이 fixheap이다 !

3. fixheap 하자

 - 이제 루트노드로 올라온 가장 오른쪽에 위치한 리프노드가 다시 자기 자리를 찾아가야 한다.

 - 자식노드들 중 값이 큰 노드와 자신을 비교해서 자신이 더 작다면 그 노드의 위치로 내려간다 (그 자식노드는 올라옴)

 - 이 과정을 자신의 위치를 찾을 때 까지 반복하여 수행 한다.(recursive하게)

 - 한번의 과정에 2번의 연산 수행 (자식들 끼리 누가 더 큰지 비교, 그 큰 자식과 자신과 비교 )

 - full binary tree 이므로 h = log n  ---->  W(n) : 2logn -->Θ(logn)

4. Algorithm

지금까지 입력으로 부터 힙이 구성된 상태에서 sort를 어떻게 할 수 있는지 에 대하여 배웠습니다.

(2)에서는 입력으로 부터 heap을 어떻게 construct하고 성능분석과

힙소트의 성능을 올릴 수 있는 방법에 대하여 알아봅시다.