대엉코딩

오늘은 프로그래머스 해쉬문제를 풀면서 하나 알게된 사실이 있습니다..

c++ algorithm 라이브러리 sort()를 이용할 경우

문자열은 사전 순으로 정렬이 된 결과가 나옵니다.

unordered_map의 경우 잘 안써와서 미숙한데, 그래도 알아두어야 겠다 생각하여 따로 작성해서 

게시글로 올려야 겠네요....! 

www.acmicpc.net/problem/1620

1. 풀이방법

- 포켓몬도감을 입력받아 찾으면 되는 문제입니다.

- 첫번쨰 문제는 입력이 숫자 일수도, 포켓몬 이름 일수도 있다는 것입니다.

- 이름의 경우 알파벳만으로 이루어져있다고 했으므로, 입력받은 문자열의 첫글자가 알파벳인지 숫자인지만

- 구분해서 구하여주었습니다.

2. 주의사항

- 처음에 그냥 선형탐색으로 짰는데, 이 경우 최대연산 수가 대략 10,000,000,000이 되므로 시간조건을 만족x

- 결국 이분탐색을 이용하고자 하였고 그러려면 알파벳순으로 정렬을 해야 하는데 , 그러면

- index가 섞이기 때문에 따로 알파벳입력이 들어왔을 떄를 위한 index도 가지고 있는 배열을 선언하였습니다.

- 숫자가 들어올 경우 vector<string> 을 통해 index를 구해서 바로 접근 하였고,

- 알파벳으로 들어올 경우 vector<pair<string,int>> 를 정렬해놓은 것을 통해 이분 탐색으로 찾았습니다.

3. 나의코드

#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
#include<queue>
using namespace std;

vector<string> dokam;
vector<pair<string, int>> dokamname; //알파벳이 입력되었을 경우 이분탐색을 위한 !
string tmps;
void find(int bot, int top) {
	if(bot>top) return;
	int mid = (bot + top) / 2;
	if (tmps == dokamname[mid].first) { cout << dokamname[mid].second << '\n'; return; }
	else if (tmps < dokamname[mid].first) { find(bot, mid - 1); }
	else { find(mid + 1, top); }
}
bool compare(pair<string, int> &a, pair<string, int> &b) {
	if (a.first < b.first) return true;
	else return false;
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	int n, m;
	cin >> n >> m;

	for (int i = 1; i <= n; i++) {
		string s;
		cin >> s;
		dokam.emplace_back(s);
		dokamname.push_back({ s,i });
	}
	sort(dokamname.begin(), dokamname.end(), compare);
	while (m--) {
		int result = 0;
		cin >> tmps;
		if (tmps[0] >= '0'&&tmps[0] <= '9') { //숫자일경우
			int deci = 1;
			for (int i = tmps.length() - 1; i >= 0; i--) {
				result += deci * (int)(tmps[i] - '0');
				deci *= 10;
			}
			cout << dokam[result-1] << "\n";
		}
		else { //선형탐색으로는 시간초과 -> 이분탐색 진행
			find(0,n-1);
		}
	}

	return 0;
}

www.acmicpc.net/problem/10825

1. 풀이방법

- algorithm 라이브러리 내에 정의되어있는 sort를 사용하였습니다.

- 이를 사용한다는 가정하에 cmp함수를 원하는 대로 작성할 수 있는지를 물어보는 문제인 것 같습니다.

- 조건 그대로 작성해주시면 됩니다.

- 코드의 길이를 줄일 수 있지만 저는 보통 아래의 코드의 형식을 벗어나게 작성하지는 않습니다.

- 이 문제처럼 이것만을 물어보기 위한 경우가 아닌 경우 보통 이렇게까지 분류조건이 많이 달리지는 않는데 그랬을 때

  코드 한 두줄 정도 더 길지만 저 같은 경우 의미 파악이 그게 더 분명히 되서 실수할 가능성도 줄고 해서 그대로 작성

  하는 편입니다.

2. 주의사항

- 증가순, 감소순 정확히 구별

3. 나의코드

#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
using namespace std;

int N;
struct studentscore {
	int kor; int eng; int mat;
	string name;
};
vector<studentscore> studentarr;

bool cmp(studentscore s1, studentscore s2) {
	if (s1.kor > s2.kor) { return true; }
	else if(s1.kor==s2.kor){
		if (s1.eng < s2.eng) return true;
		else if (s1.eng == s2.eng) {
			if (s1.mat > s2.mat) return true;
			else if (s1.mat == s2.mat) {
				if (s1.name< s2.name) return true;
				return false;
			}
			else return false;
		}
		else return false;
	}
	else return false;
}

void inputs() {
	cin >> N;
	for (int i = 0; i < N; i++) {
		studentscore tmps;
		cin >> tmps.name >> tmps.kor >> tmps.eng >> tmps.mat;
		studentarr.push_back(tmps);
	}
}
int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
	inputs();
	sort(studentarr.begin(), studentarr.end(), cmp);
	for (int i = 0; i < studentarr.size(); i++) {
		cout << studentarr[i].name << "\n";
	}
	return 0;
}

0. 알아보기전에....

 - 지금까지  insertion sort,  quick sort, merge sort, heap sort 등....

    에 대해서 알아보았습니다.

 - 이러한 sorting 알고리즘들은 모두 두 수의 대소비교(key value에 대한) 를 하여 sort를 하는 class 의 알고리즘입니다.

 - 두 수의 크기비교를 통해 정렬하는 알고리즘은 최적의(optimal) 알고리즘은 O(nlogn) 이라는 것도 확인 하였습니다.

1. radix sort (기수정렬)

 - 먼저 언급하자면 , 이 sorting 알고리즘은 O(n) 이라는 수행시간을 가집니다.

 - ?????? 최적은 O(nlogn) 이라는 것도 증명 하였는데 어떻게 O(n)에 수행하는 sorting 알고리즘이?!

 - 그 이유는  크기비교가 아닌 다른 연산을 사용하기 때문에 class가 다른 algorithm이기 때문입니다.

 - 즉 , 두 수간의 대소비교를 통한 어떠한 방법으로 정렬을 하는 것이 아니라는 뜻이죠

2. Strategy 

 - 그럼 어떻게 할 것인가.......?

 - 선생님이 50명의 학생의 시험지를 점수별로 정렬을 시키고 싶은 상황이라고 해보자. (점수는: 0~99 <편의상>라 하자)

 - 일단, 0.1.2.3.....9 까지가 적혀있는 박스 10개를 준비하자.

 - 그리고 1의자리 수 를 기준으로 박스에 담자.

 - 그 후 0번 박스부터 9번 박스까지 들어있는 종이를  다시 하나의 뭉텅이로 합친 후

 -  이제 10의자리 수 를 기준으로 다시 0~9번 박스에 나누어 담자.

 - 모든 점수는 최대 2자리 수 이므로 2번의 이 작업을 수행 하면 sorting이 완료 된 상태이다.

 - 여기서 생각해보면 박스에 맞는 숫자를 담았을 뿐 두 수끼리의 비교하는 연산은 수행하지 않았다 !

 - 이렇게 할 수 있었던 이유는 무엇 일까? 자료에 대한 정보가 더 있었기 때문에 가능했다.

    (이 경우에는 점수 의 범위를 추가적으로 알고 있었다.)

 - **stable**

  : 이 알고리즘의 핵심 property 중 하나는 위에서(위의 상자부터) 순서대로(차례대로) 처리한다는 것

    이럴경우 stable하다고 이야기 한다.

    (즉, 같은 key값을 가진 input data가 여러개 있을 때 그 때 순서가 입력 순서와 같을 것을 보장한다는것)

     --각 단계를 수행 할 때 ! (각 단계는 stable 해야한다.)

3. Algorithm

 <list>이용

4. Analysis

 - distribute  --> Θ(n)  (숫자보고 통에넣고.....n번 수행)

 - combine  -->Θ(n) (list 내용을 하나로)

 - 이 작업을 몇번 수행 하느냐? 4자리수이면 4번....... 즉 자리수 (d) 만큼 (linear in n)

 - O(n)

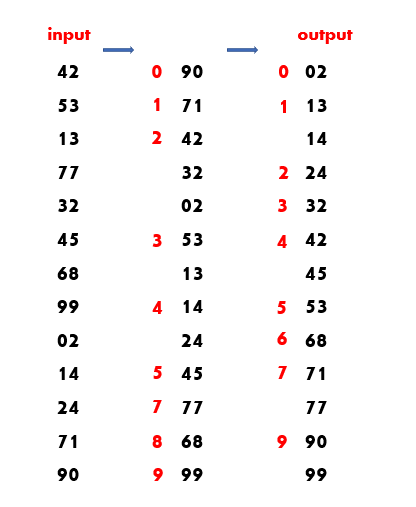
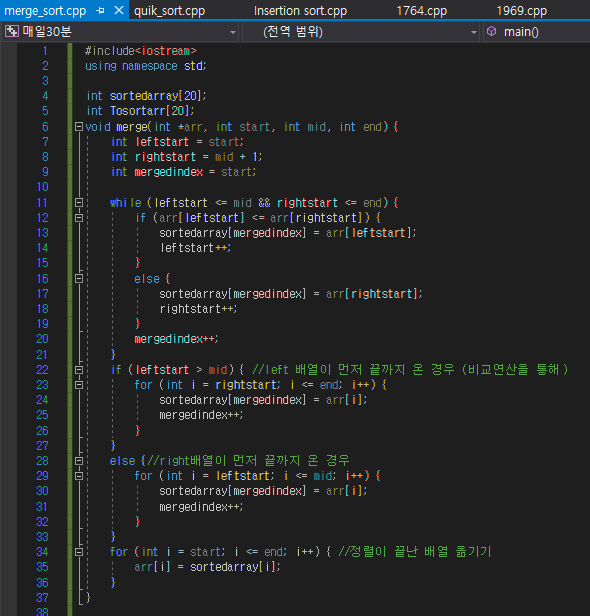
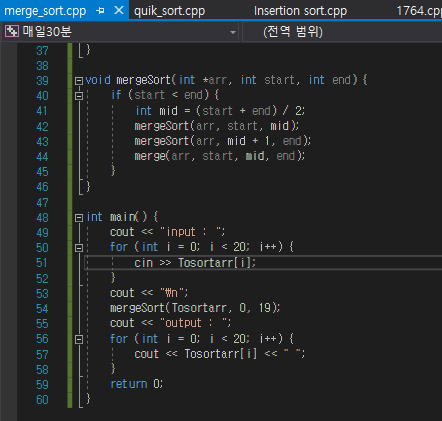
1. constuct Heap

 - heap sort를 위해서는 일단 입력으로 들어온 배열을 heap의 조건을 만족 하도록 만들어 줘야한다. (구조,순서)

 - 중요한 것이 있는데 heap의 구조조건은 full binary tree 이기 때문에 사실 입력(배열) 자체가 구조조건을

   만족한다.

 - 그럼 우리는 순서 조건만 맞춰서 힙을 구성하면 된다 ! 어떻게 할 것인가? 

 -밑에 자식쪽의 서브트리는 heap조건을 만족 할 때 위와 같이 하나의 노드를 삽입하면

 -순서조건이 check 되지 않은 노드는 단 하나뿐이다. --> 이 노드에 대해서 fixheap을 수행 하면

 n+1짜리의 heap이 완성 된다. (이 과정은 O(logn) -->하나의 원소를 heap에 삽입하는))

 - 이 아이디어로 밑에서부터 heap을 구성해 나가는 것이다.

2. Analysis

 - 이제 힙을 구성하고 sort 하는 것 까지 알아보았다 .... 성능 분석을 해보자 !

 - 먼저 heap construction 부분에서 짚어보자.

- 언제가 최악의 경우? (Worst case) ---> construct힙을 하는데 계속 그 노드의 위치가 leaf노드 일 때 이다

  (끝까지 내려갈 때) 

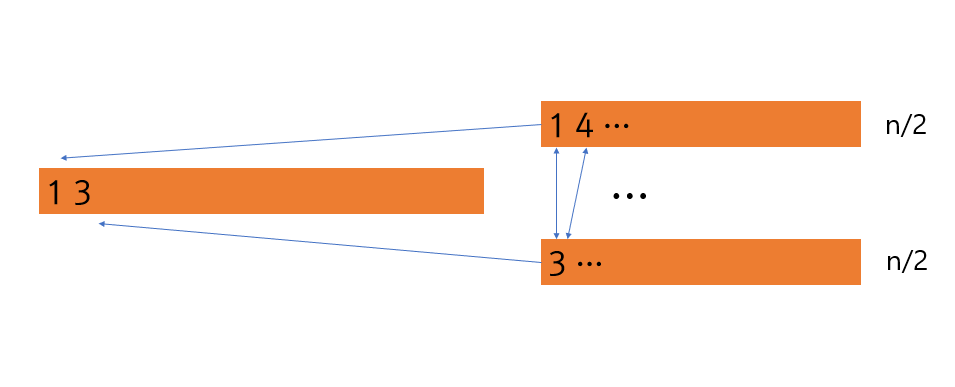
- 각 노드가 삽입 될 때 (heap을 구성하기 위해) 자신의 자리를 찾아 갈 때 규칙을 한번은 오른쪽으로 내려가고

   그 이후에는 쭉 왼쪽으로 내려간다고 하자.

 - 저렇게 내려갈 경우 힙을 다 구성 했을 때 leaf노드로 내려간 간선이 겹쳐지는 일이 없다 !

    (서로 다른색이 지나갈 때 지나간 간선을 다른 노드가 지나갈 때 그 간선을 지나가는 일이 없다)

 - construct heap 과정에서 하는 총 비교연산의 수 <= 2(비교연산) * n-1(간선의 수) ---> O(n)

 - heap sort의 최악의 경우 --->  O(2nlogn)  (sort)   +   O(n) (힙 구성)  -->  O(nlogn) 이다

 - 대소비교 연산을 이용한 sorting의 경우 O(nlogn)보다 빠를 수는 없으므로 optimal 이라고 할 수 있다.

3. Accelerate Heapsort (BubbleUpHeap)

-- > heap sorting  과정에서 fixheap을 할 때 각 단계에서 노드는 두번의 비교연산을 수행했었다.

      ( 둘 중의 누가 더 큰 자식인가 )  +  (본인과 더 큰 자식과의 비교)

- 이렇게 매번 내려갈 때 마다 두번의 비교연산을 하지 말고 한번 (둘 중의 누가 더 큰 자식인가)

   만 비교하고 무조건 그 큰 자식 쪽으로 내려간다 ( 언제까지? h/2 즉 절반정도 내려올 때 까지 )

- h/2 정도 까지 내려왔을 때 부모 노드와 비교연산을 한번 실시한다..!

- 1) 부모노드가 더 크다면? (조건만족) -->다시 나머지 h/2에 대해서 recursive 하게 다시 수행

      --> 다음엔 h/4만큼 가고 다시 비교하고...또 reculsive....!

  2) 부모노드가 작다?? --> 너무 많이 내려왔다....비교를 통해 다시 위로 올라가 내 자리를 찾아간다.

3-1 Accelerate Heapsort Analysis

 - 연산의 수를 살펴보자 (최악의 경우)

 - h/2 (이만큼 한번의 연산을 통해 내려온다) + 1(부모노드와 비교) + h/4 (다시 진행) +1 ......

   <= h (h/2+h/4+.......) + logh (1+1+...... --->log 높이)  라고 할 수 있겠다 

 - h= logn 이다 즉 . 이 방법을 통해 서 우리는

 - worst case가 nlogn+Θ(nloglogn) 임을 알 수 있다.

 -점근 분석을 하면 최악의 경우는 앞에서 본 힙소트(O(2nlogn)) 과 O(nlogn+nloglogn) 모두 O(nlogn) 이지만

 - 비교 연산의 수는 절반 정도 줄여서 성능을 향상 시킬수 있다고 생각할 수 있다.

0. heap?

 - 구조 조건과 순서 조건을 가지고 있는 자료구조 이다.

 - 구조 조건 : 이진트리인데 갚이가 h 일 때 h-1까지는 full binary tree 이고 h번째에는 왼쪽부터 차례대로 채운다.

 - 순서 조건 : 부모노드는 자식노드 보다 크다 (max-heap 일 때) , 직계가 아닌 노드 끼리는 상관이 없다.

1. heap sort?

 - 위에서 언급한 heap 이라는 자료구조를 이용한 sort 방법이다.

 - heap의 특성을 생각 한다면 ? n개의 정보를 sort하기 위해선

 - data를 heap 구조로 construct 하면 root 노드 에 있는 값이 가장 큰 값이므로 그 값을 빼오면 된다. 

    (n번의 삭제연산을 수행 하면 sort가 완료된다.)

2. delete(root) and fixheap ? (downheap)

 - 루트에 있는 노드(제일 큰값을) 가져갔다고 하자. 그러면 남은 노드들로 다시 heap을 만족하도록

   트리를 구성해야 그 다음 루트노드를 또 삭제할 수 있다 (두 번째로 큰값이겠죠? 전체에서? )

 - 그렇다면 생각 해보자 ..... 루트를 제외하고 남은 트리에서 heap이 되게 하려면

 - 구조 조건과 순서 조건을 만족해야 하는데...... 어떤 것을 만족하는게 더 쉬울까 ? ----> (구조조건?)

 - 왜?? 만약에 n-1개의 노드가 남아 있다고 할때 heap의 구조조건을 만족하도록 만드는 모양은 하나뿐이다.

    ( 즉 위치로 보자면 어디 위치의 노드가 없어지느냐 ? 맨 밑 리프 노드 열에서 가장 오른쪽의 노드 !)

    ( 이 위치는 O(1) 에 바로 찾을 수 있다...! ....왜? heap은 배열로 구현 하기 때문에 맨 마지막 index의 노드!)

 - 그럼 일단 가장 오른쪽에 위치한 리프노드를 루트 노드로 덮어 쓰자 ! --->구조 조건은 만족 !

 - 이제 순서조건을 생각해보자 .... 일단 루트노드로 덮어쓴 가장 오른쪽 리프 노드가 다시 자신의 자리를 

 - 찾아갈 수 있도로 해야 하는데 이 과정이 fixheap이다 !

3. fixheap 하자

 - 이제 루트노드로 올라온 가장 오른쪽에 위치한 리프노드가 다시 자기 자리를 찾아가야 한다.

 - 자식노드들 중 값이 큰 노드와 자신을 비교해서 자신이 더 작다면 그 노드의 위치로 내려간다 (그 자식노드는 올라옴)

 - 이 과정을 자신의 위치를 찾을 때 까지 반복하여 수행 한다.(recursive하게)

 - 한번의 과정에 2번의 연산 수행 (자식들 끼리 누가 더 큰지 비교, 그 큰 자식과 자신과 비교 )

 - full binary tree 이므로 h = log n  ---->  W(n) : 2logn -->Θ(logn)

4. Algorithm

지금까지 입력으로 부터 힙이 구성된 상태에서 sort를 어떻게 할 수 있는지 에 대하여 배웠습니다.

(2)에서는 입력으로 부터 heap을 어떻게 construct하고 성능분석과

힙소트의 성능을 올릴 수 있는 방법에 대하여 알아봅시다.

1. 기본 개념

 - 만약 순서대로 정렬된 두개의 배열 이 있다고 생각해보자.

 - 이 두 배열을 합쳐서 정렬된 배열을 얻고자 할때는 첫번째 elemet끼리의 비교만을 반복하면 된다.

    (둘 중 하나의 배열이 끝날때 까지만)  ---> 즉 가장 많이 비교할때는 (지그재그) n-1, 적게는 n/2 이다.

//지금 까지 설명한 것이 병합(merge) 과정이다.

2. mergesort의 대표적인 특징 

 - divide and conquer 전략을 이용하는 대표적인 알고리즘이다.

 - 원소들 끼리 대소를 비교해서 정렬하는 알고리즘 중에서는 최적의 알고리즘 이다.(O(nlogn))

3. MergeSort Strategy

 - 입력받은 배열을 divide 한 후 merge 한다. 

 - (merge를 하는 과정에서의 아이디어는 1에서 설명한 내용과 같다.)

 - 모두 merge를 하면 sort가 완료된 상태이다.

 - divide를 완료한 상태에서 sort를 진행하면서 Merge 하면서 올라오므로 merge가 완료 됬다면 sorted 된 상태이다.

4. Algorithm : Mergesort

5. Analysis

 위의 의사 코드를 확인 하고 분석해보면 이러한 점화식이 나온다.

 W(n) =O(1)+O(1)+W(n/2)+W(n/2)+Wmerge(n)

 (by MasterTheorem)

 =====>>> Θ(nlogn)

6. 구현

결과화면

** divide and conquer(분할 정복) 은 알고 들어가야한다. --> 퀵소트가 사용하는 기법

1.Quick-sort

 - random 한 속성을 가진 형태의 input을 정렬하는 데 성능이 매우 좋다.

 - pivot 이라는 하나의 element를 기준으로  L(less), E(equal), G(greater)로 나눈다 (분할)

 - 나눈후  L 과 G(E U G) 로 다시 recursive하게 sort를 수행한다.

2. Worst Case

 - 최악의 경우 pivot을 잡고 분류를 하는 과정에서 L,G를 나누는데 계속 한쪽으로 몰리는 경우 이다

 - 이럴경우 n-1번을 나누게 되고 (depth = n), 각 단계에서 약 n, n-1, n-2 ....... 1까지 진행되므로

 - running  time의 합은 n+(n-1)+ ... +1 이므로 최악의 경우 O(n^2) 이다.

3. Average Case

 - 평균분석의 경우 O(n*logn) 이다.

 - 최악의 경우는 느리지만 평균분석은 상당히 빠르다.

4. 알고리즘

-partion 별 

5. 특징

 - partion을 한번 하면 pivot은 자신의 위치를 찾는데 그 자리가 최종 출력 위치이다.

 - in-place 로 구현 가능 (추가적으로 사용하는 메모리가 tmp변수 하나 정도로 O(1) 정도

6. 구현