대엉코딩

* 이진 탐색 트리?

 - 검색에 많이 사용이 되는 형태입니다.

 - 중위 순회 (Inordered traversal)를 할 경우 key값에 따라 sorting된 결과를 얻을 수 있습니다.

    # 구조 조건

     - 각 노드들은 자식노드를 기껏해야 두 개만을 가질 수 있습니다.

    # 순서 조건

     - 각 노드들의 왼쪽 서브트리에 있는 노드들은 각 노드보다 작은 값을 가집니다.(key)

     - 각 노드들의 오른쪽 서브트리에 있는 노드들은 각 노드보다 큰 값을 가집니다.(key)

    # 중위 순회

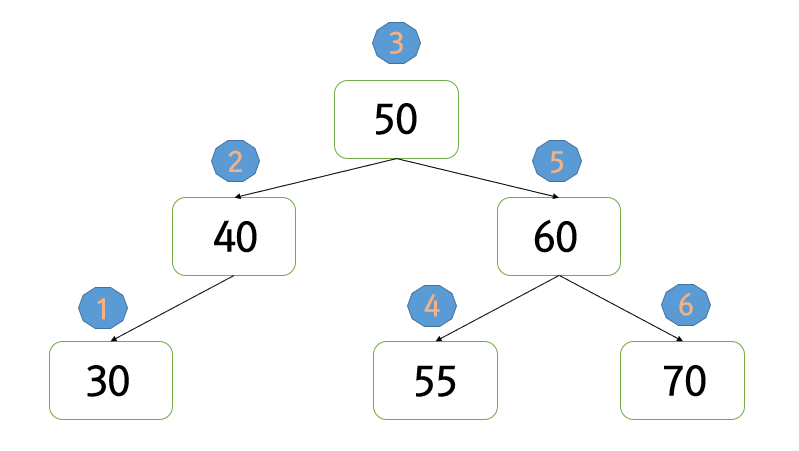
구조 조건과 순서 조건을 만족하는 이진탐색트리를 구성(construct) 하였다면

위와 같이 inordered traversal을 하면 key값을 기준으로 정렬이 됩니다.

(30,40,50,55,60,70)

 * 탐색연산(search)

 - root 노드 부터 시작하여 탐색하고자 하는 값 n 과 비교를 하며

   비교하는 노드보다 n값이 작다면 왼쪽 서브트리로 가서 왼쪽 서브트리의 루트노드와 다시 비교.

   비교하는 노드보다 n값이 크다면 오른쪽 서브트리로 가서 오른쪽 서브트리의 루트노드와 다시비교를 하면 됩니다.

* 삽입연산(insert)

 - 삽입연산은 탐색연산과 같이 내려가다가 자기 자리를 찾아서 들어가면 됩니다

 - 위의 저의 예시는 나름 예쁜? 모양이지만 이진탐색트리의 구조 조건과 순서 조건만 만족 하면서 구성해 나가면됩니다.

 - 같은 노드들의 값과 수 여도 다양한 모양의 이진탐색트리가 나올 수 있습니다.

 - 역시나 이와 같은 경우에도 순서와 구조 조건이 모두 맞습니다 --> 중위순회를 하여도 결과가 그대로 나옵니다.

 * 삭제연산(delete)

 - 이진탐색트리는 어떠한 노드를 삭제연산을 수행하여 제거 하여도 그 결과의 트리 역시 이진탐색트리여야 합니다.

    (당연하죠? ㅎ)

 - 두 경우로 나누어서 보겠습니다.

    1.) 삭제하려는 노드의 두 자식노드가 leaf노드인 경우입니다. --->그냥 삭제해버리면 됩니다.

    2.) 삭제하려는 노드의 자식이 하나는 leaf노드이고 한쪽은 서브트리(노드)를 가지는 경우

       - 삭제하려는 노드의 자리에 한쪽 서브트리를 연결 해주면 됩니다.

    3.) 두 자식이 모두 leaf노드가 아닌 값을 가진 노드 들( 즉, 두개의 서브트리를 가지는) 일 경우

        -- 본 예에서 60을 삭제 하고자 한다고 가정 하겠습니다. delete(40)

        -- 위의 예에서 보고 이렇게 하면되지 , 쉽게 보일 수 있지만 아래의 예를 보면 약간은 생각보다 복잡합니다.

        -- 두가지 방법이 있습니다(succesor를 삭제노드위치에 위치, predecessor을 삭제 노드 위치에 위치)

           더 금방 찾을 수 있는 (왼쪽 서브트리의 첫번째 노드) succesor를 이용합시다.

        -- succesor를 찾아서 삭제하려는 노드의 위치에 위치 시키고 부모노드와

        -- 삭제한 노드의 subtree들과 successor를 연결 시켜 주시면 됩니다.

        -- 위와 같이 삭제 연산을 수행 한 뒤에도 이진탐색트리가 나오게 되었습니다.

 * 성능분석

 - search, insert, delete (탐색, 삽입, 삭제) 연산 모두 O(n) 입니다.

 - worst case는 편향된(즉, 한쪽으로만 쭉쭉 뻗어있는 ) 트리입니다. 

 - tree에서의 연산들은 tree의 depth와 연관이 되어있는데 이럴경우 depth가 n(n-1) 이기 때문입니다.

 - average case의 경우 O(log n) 인데 worst case도 O(log n ) 을 맞추고 싶을 경우

 - depth를 맞추어주기 위해서 어느정도 균형이 잡혀 있는(예뿌장한?) 트리를 만들어 주어야 합니다.

 - 대표적인 균형이진트리들은 AVL TREE, RED-BLACK TREE 등이 있습니다.

1. 삽입정렬(insertion sort) 란?

 - 각 단계 마다 하나의 원소를 그 앞의 원소들과 비교를 해서 자신의 자리를 찾아 가는 것이다.

 - 첫 번째 원소는 처음에는 혼자이므로 그 자체로 정렬된 상태이고 두번째 원소부터 비교를 하며 정렬을 한다

 - 첫번째 와 두번째 원소를 비교를 제대로 했다면 3번째 원소를 정렬 할때는 3번째 원소 앞쪽은 정렬이 되어있는 상태일 것 이다.

 - 그럼 세번째 원소가 이제 자신의 자리를 찾으러 갈 것이고 네번째 원소가 비교를 시작하려 할 때는 앞의 3개의 원소는 정렬된 상태

 - 그리고 비교를 해가면서 원소의 자리가 바뀔 수 있기 때문에 자신의 차례때 배정받은 위치가 최종출력의 위치는 아니다.

2. 최악의 경우 (worst case) 

 - 키 오름차순 정렬을 하고 싶다고 가정했을 때, 계속 키가 제일 작은 사람이 차례대로 들어오는 것이다.

   ( 즉, 입력이 역순으로 정렬되어 있을 때)   -->  Θ(n^2)

3. 평균의 경우 (Average Analysis)

 - 각 자리에 들어갈 확률은 모두 같다고 가정 (1/i+1) -->>내가 원소로 들어갔을 때 그자리도 포함 i+1

 - step i에서 평균 i/2의 연산

 - 평균 분석의 경우 대략 n^2/4 정도 이다. 

4.특징

 - input의 크기가 적을 때에 한정해서 매우 빠르다고 알려져있다.

 - 한번에 잘못된 위치를 하나만 수정할 수 있는 제한적인 조건 내에서는 최적의 알고리즘 이다.

5. 구현 (key값을 그냥 입력받은 int의 수라고 가정하고 , 그냥 vector<int>의 각 index에 해당하는 값을 통한 정렬을 구현)

https://www.acmicpc.net/problem/3986

- 조건1. 같은 문자끼리 연결한 선이 교차 하지 않아야 한다.

- 조건2. 각 글자를 정확히 한개의 다른위치에 있는 다른글자와 짝지을 수 있다.

- 문제를 읽고 조건을 생각해보다가 스택을 이용하면 편하게 풀수 있다고 생각한 것이

- 스택에 넣어놓고 같은 단어가 들어와서 그 단어와 함께 pop이 되면 그것이 선이 교차하지 않는다는 것으로 생각

- 1. 스택이 비어있으면 삽입

- 2. 스택의 top()과 현재 문자가 같으면 스택을 pop()

- 3. 스택의 top()과 현재 문자가 다르면 그대로 스택에 push()

- 단어 전체를 순회 하는동안 위 과정을 거쳐는데 만약 1번 조건이 만족하지 않는다면 스택에서 빠져나가지

- 못한채로 남아있는 문자들이 있을 것이고 1번은 만족해도 2번이 만족되지 않는다면 홀수개의 문자가 스택에 남아있을

- 것입니다.

- 즉 반복문을 모두 돌았을 떄 스택이 비어있어야 그 단어는 좋은 단어 인것입니다.

<필기>

<코드>