대엉코딩

오늘은 적성시험을 보느라 많은 걸 하진 못했지만...^

요즘 문자열관련 문제를 좀 풀어보고 있는 중입니다..

c++ string 에서 push_back(char c) 즉 push_back은 쓸수 있지만 한글자만 넣을 때 사용가능

문자열을 붙일 경우 그냥 + 를 사용해서 뒤에 붙이시면 됩니다.

string to int --> stoi(string)

int to string --> to_string(int) 

사용

간단하게 정리했습니다

오늘은 프로그래머스 해쉬문제를 풀면서 하나 알게된 사실이 있습니다..

c++ algorithm 라이브러리 sort()를 이용할 경우

문자열은 사전 순으로 정렬이 된 결과가 나옵니다.

unordered_map의 경우 잘 안써와서 미숙한데, 그래도 알아두어야 겠다 생각하여 따로 작성해서 

게시글로 올려야 겠네요....! 

www.acmicpc.net/problem/1254

1. 풀이방법

- 일단 처음 문제를 읽고 든 생각은 제일 길어봤자 문자열의 길이 *2 정도 이겠구나 였습니다.

   (뒤에서부터 차례대로 추가하면 되니까)

- 입력은 string으로 받아 편의를 위해 저는 vector<char>에 옮겨 담았습니다.

- 그리고 이제 하나씩 추가를 하고 이게 펠린드롬이 맞는지를 확인하였습니다.

- 반복문만 활용하면 잘 풀 수 있는 문제였습니다.

2. 주의사항

- 없음. 

3. 나의코드

#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
using namespace std;

string s;
vector<char> carr;
vector<char> tmpc;
int resultlen;

bool isitpelen() {
	for (int i = 0; i < tmpc.size() / 2; i++) {
		if (tmpc[i] != tmpc[tmpc.size() - 1 - i]) return false;
	}
	return true;
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> s;
	for (int i = 0; i < s.length(); i++) carr.push_back(s[i]);

	resultlen = s.length();
	tmpc = carr;
	if (isitpelen()){
		cout << resultlen << "\n"; return 0;
	}
	for (int i = 0; i < s.length(); i++) {
		tmpc = carr;
		for (int j = i; j >= 0; j--) {
			tmpc.push_back(s[j]);
			if (isitpelen()) {
				cout << resultlen + i + 1 << "\n"; return 0;
			}
		}
	}
	return 0;
}

www.acmicpc.net/problem/1439

1. 문제풀이 방법

- 0과,1 의 그룹을 묶어서 더 그룹이 적은 쪽을 뒤집어 줘야 적은 횟수로 통일을 할 수 있다.

2. 주의사항

- 전 어려운 문제인줄 알았던게 문제를 잘못읽어서 연속된 두 숫자 이상 뒤집을 수 있다는 건줄 알았습니다;;

- 0010 의경우 1은 하나라서 못뒤집어서 앞에 00을 뒤집고 1110을 만든뒤 다시 111을 뒤집어 0000을 만들어야

되는 줄 알고 꽤나 머리를 굴렸는데....알고보니 매우 간단한...문제.......문제를 꼼꼼히 똑바로 읽자 !

3.나의 코드

include<iostream>
#include<string>
#include<algorithm>
using namespace std;


int count0;
int count1;
int resultcount;
int main() {


	string inputs;
	cin >> inputs;
	if (inputs[0] == '0') { count0++; }
	else { count1++; }

	int nows=inputs[0];

	for (int i = 1; i < inputs.length(); i++) {
		if (inputs[i] != nows) {
			if (inputs[i] == '0') { count0++; nows = inputs[i]; }
			else { count1++; nows = inputs[i]; }
		}
	}
	cout << min(count0, count1) << "\n";
	return 0;
}

1.개요

- 보이어모어 알고리즘 역시 kmp 알고리즘과 마찬가지로 패턴과 텍스트 중 패턴을 preprocessing 하는 방식이다.

- kmp 알고리즘과는 반대로 패턴을 텍스트의 특정 위치에 놓고 비교를 할 때

  kmp는 패턴의 앞 쪽부터 차례대로 비교를 시작하는 반면 (왼쪽에서 오른쪽)

  보이어모어는 패턴의 뒤 쪽부터 차례대로 비교를 시작한다. (오른쪽에서 왼쪽)

2.아이디어

- 브루트포스 방식과 어떤차이점을 가지고 수행시간을 단축시켜주느냐~ 인데.

- 보이어모어 알고리즘에서는 두가지의 큰 아이디어가 있다.

    -> Looking-glass heuristic

        : 패턴의 뒤 쪽부터 비교를 시작한다.

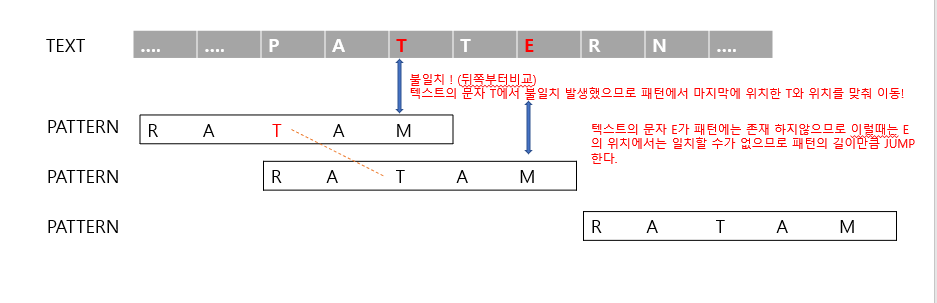
    ->Character-jump heuristic

        : 패턴을 구성할 수 있는 모든 글자의 마지막 발생위치를 미리 구해서 테이블 형태로 저장해 놓는다.

          텍스트와 패턴을 뒤쪽에서부터 비교해 오다가 불일치 발생시 그 때 위치의 텍스트 문자가 패턴의 마지막에 등장한 문자의 위치를

          맞춰 패턴을 옮긴다.

이해하기 위한 간단한 이론적 예시는 아래와 같다.

3. 전처리(preprocessing)

- 2번에서 말씀드렸다싶이 전처리 과정은 매우간단하며 패턴을 한번 쓱 스캔하면 되므로 시간도 오래걸리지 않습니다.

- 앞에서부터 보면서 뒤쪽에 등장할 때 마다 그 위치로 문자열테이블을 업데이트 해주시면 되겠습니다.

- 처음에 테이블을 만들어 -1로 초기화 시키고 위의 작업을 수행하면 전처리후에도 여전히 -1값을 가지는 문자는 텍스 

  트에는 있을 수 있으나 패턴에는 존재하지 않는 문자이므로 이 경우 패턴의 길이만큼 jump를 해주시면 되겠습니다.

4.The BoyerMoore Algorithm

-주의 해야할 점 하나는

  mismatch가 발생한 위치에 있는 문자가 현재 패턴의 문자열 위치보다 뒤쪽에 있을경우

  그대로 옮겼다가는 패턴이 다시 앞쪽으로 갈 수 있고 무한반복과 중복 처리 등이 발생할 수 있다.

  이 경우는 그냥 한칸 뒤로만 옮겨주는 것으로 대체한다.

5. 분석(Analysis)

- 시간 복잡도 : O(n*m+s)

- 최악의 경우를 분석해보면 심지어 브루트포스방식의 시간복잡도인 O(n*m)보다도 s만큼의 시간이 더 걸린다.

- 최악의 경우 예시를 보자면

        TEXT= aaaaaaaaaa........a

        PATTERN = baaa

-최악의 경우는 문자의 범위가 좁은 DNA Sequence나 이진문자열 같은 곳에서는 발생할 확룰이 꽤 있다.

- 하지만 영어 알파벳이나 한국어 처럼 문자의 범위가 매우 큰 경우 매우 효율적으로 빠르게 동작한다.

0. 개요에 앞서....

-보통 string matching 문제를 해결하는 방식은 크게 두가지가 있는데

  -1. pattern을 preprocessing하는 방법

  -2. text를 preprocessing하는 방법

- 지금부터 살펴 볼 kmp나 booyer moore 알고리즘은 모두 패턴을 preprocessing하는 방식이다.

- text 자체가 잘 변하지 않거나 규모가 엄청 클 때는 2번의 방식을 사용하기도 한다.

1. 개요

- Knuth-Morris-Pratt's의 알고리즘 역시 브루트포스방식과 마찬가지로 왼쪽에서 오른쪽으로 텍스트와 패턴을 비교해 나가는 방식이다.

- 하지만 패턴을 옮길 때 브루트 포스보다는 조금 더 효율적인 방식을 사용한다.

2. 아이디어

- 브루트포스 방식에서 발생하는 중복되는 비교연산을 피하기 위해 kmp 에서는 

- 패턴을 preprocessing하는 과정을 먼저 진행해서

- 패턴 비교가 실패한 지점에서 suffix중 가장 긴 prefix와 일치하는 지점을 찾아내서 이것은 비교하지 않고 건너뛴다.

- 말로 들으면 무슨말 인가 싶지만...

- 브루트 포스와 비교를 해보면 브루트포스방식에서는 단순히 패턴을 한칸 옮겼을 것이다.

  그것과 비교해볼 때 kmp는 좀 더 효율적으로 패턴을 이동시켜 비교연산 횟수를 줄인다 !

- 그리고 prefix와 suffix가 일치하는 최대길이를 계산하여 이동시키므로 이동시킨위치보다 이전의 위치의 텍스트에서는 

   패턴이 발생할 수 가 없다!

3.preprocessing

- 이제 위의 아이디어를 사용하기 위해서는 패턴을 전처리를 해서 필요한 정보를 저장해두어야 할 필요가 있다.

- 보통 kmp failure function이라고 하는데, 패턴의 각 위치에서 prefix와 suffix가 일치하는 최대길이를 미리 계산해서 테    이블 형태로 저장해놓고 필요할 때 이 값들을 리턴해주는 함수이다.

- 처음에는 눈과 손으로 직접 비교하면서 값들을 확인해보는 것을 추천드립니다.

- A , AB, ABA, ABAA, ABAAB, ABAABA 식으로 확인을 해보시면 됩니다.

4. 수도코드

- Failure Function

- KMP algorithm

5. 시간복잡도

- failure function은 최대 2m번의 비교를 통해서 구할 수 있으므로 O(n)

- 같은 방식을 사용하는 kmp는 failure function을 구하는 과정을 포함하여

   O(n+m)의 시간복잡도를 가진다.

- 이는 브루트포스 방식의 O(m*n)에 비해서 매우 빠른 속도이다.

0. string

- character의 sequence 이다.

- string의 예시로서는

  -> HTML문서

  -> DNA sequence

  -> 등등....매우 많다.

- 아스키코드, binary alphabets, DNA alphabets( {A,C,G,T} )

- 보통 TEXT에서 PATTERN과 일치하는 SubString(그 위치)를 찾는 문제가 많다.

- 검색엔진, 텍스트 에디터, 생물학적 조사 등 을 할 때 주요하게 사용된다. 

1. 개요

- 가장 간단하고 naive한 방식의 알고리즘 이다.

- 텍스트의 위치 가능한 모든 자리에 PATTERN을 매치시켜 비교과정을 거친다.

- 비교과정 중 완벽하게 매치하거나 남은 텍스트의 길이보다 패턴의 길이가 더 길어질 경우 비교를 멈춘다.

2. 시간복잡도

- 워낙 간단해서 의사코드를 기재하진 않았지만 복잡도 분석을 해보면

- 텍스트의 길이 (m) 패턴의 길이 (n)  이라 하면 시간 복잡도는 O(n*m)

- m의 위치 가능한 모든 자리에서 n을 비교하기 때문에 최악의 경우 O(n*m) 이다.

- 최악의 경우 중 간단한 예시를 들어보면

 -> TEXT: AAAA........B

 -> PATTERN: AAAB

-이경우 불일치가 패턴의 맨 끝에 존재하므로 패턴을 매번 비교할 때 마다 끝문자가 나타날 때 까지 비교를 해야한다.

3. 장점 및 단점

- 장점은 알고리즘 자체가 매우 간단하다.

- 패턴이나 텍스트를 Preprocessing하는 과정이 없다.

- 알파벳의 범위가 좁을 경우 (위의 경우 처럼 a,b) 성능이 떨어진다.

- 영어나 한국어처럼 글자의 종류가 매우 많을경우는 나름 brute-force도 성능이 괜찮을 수 있다.