2887번: 행성 터널
첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이
www.acmicpc.net
1. 풀이방법
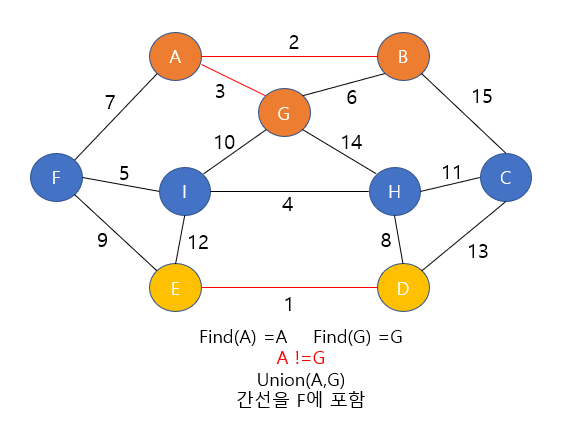
- 최소신장트리 mst 를 구하는 문제이다.
- 크루스칼 알고리즘을 떠올려서 구현을 했으나 첫 제출결과.....메모리초과.....
- 이 문제에서 사실 크루스칼 알고리즘 자체를 구현하는 것은 매우 쉬웠으나
- 제출 이후 문제 조건을 파악해보니 행성의 수 N개 의 범위가 100,000이다.
- 첫 구현은 모든 간선 (n*(n-1))/2 를 모두 넣고 sorting을 돌렸으니 메모리 초과가 뜰 수 밖에.....
- 그래서 후보가 될 수 있는 간선 자체를 줄이는 방법을 만들어야 했는데, 그 답은
- min(|x1-x2|,|y1-y2|,|z1-z2|) 여기에 있었다.
- 일단 1차원을 가정하고 말해보자 행성이 1,5,6,7,24,36에 있다
- 위치 1에서의 모든 간선은 (1,5), (1,6), (1,7), .... (1,36)까지 인데 이를 모두 볼필요 없이
- 정렬된 상태에서 맞닿은 정점들을 연결하면 이것이 1차원에서의 mst이다 (1-5-6-7-24-36)
- 그렇다면 3차원에서는....? 이렇게 해도 되는건가 머리가 아팠는데...
- 일단 결론은 된다는 것. |x1-x2|에 대해서 정렬후 맞닿은 간선들을 모두 구해서 edge에 넣고
- y와 z에 대해서도 이 작업을 했다.
- 그리고 이 간선을 cost를 기준으로 오름차순 정렬을 해주는데
- 차원을 나눠서 계산을 해도 되는 이유는 예를 들자면 7-24 이 두 행성사이의 x값 차이는 17인데
- 만약 y 나 z 값의 차이에서 더 작은 차이가 있다면 그 간선도 edge 벡터내에 있을 것이고 오름차순 정렬
- 했으므로 먼저 살펴보게 되므로 상관이 없다 뒤에 7-24를 연결하는 간선은 이미 두 정점이 같은 집합 내에 있다면
- 그냥 무시하고 넘어가기 떄문, 그리고 y나 z에서 두 행성이 붙어있지 않다면??? 이라는 의문이 들었는데
- 이 역시 붙어있지 않아 직접적인 간선은 없다고 하더라도 그 사이의 다른 정점과 연결된 간선을 통해서 7-24를 연결
- 하는 간선을 살펴보기 전에 이미 같은 집합에 포함되게 된다.
- 이를 구현한 후 제출했는데 결과는 시간초과.....흠....ㅆ..
- 첫 구현한 코드의 문제점은 그냥 planet 구조체에 각각 key(즉 root) 값을 넣어서 집합이 합쳐질 경우
- 바꿔야할 key값을 가진 정점들을 모두 탐색 해서 바꿔 주게끔 되어있었다.
- 이렇게 되면 후보 간선들을 모두 보는 for문 안에서 또 다른 for문(정점을 모두 탐색하는)
- 이 있었는데 입력이 크니 시간 초과가 날 수 밖에...
- 그래서 결국 key(root) 를 저장하고 있는 vector를 따로 선언해 재귀를 통해 탐색하고 집합의 key값이 바뀌어야 할
- 경우 탐색해서 찾은 key값만 바꿔주면 되게끔 구현 하였다.
- 여기서의 key(root)값의 의미는 집합의 대표값이다(1번 집합,2번집합...)
2. 주의사항
- 수식을 통해서 간선의 수를 줄일 수 있는 아이디어를 생각하는 것.
- 입력의 규모를 잘 파악하고 구현을 시작할 것.
3. 나의코드
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
int N;
int resultsum;
struct planet { int x, y, z,idx; };
struct edges { int cost, index1, index2; };
vector<planet> parr;
vector<int> rootindex;
vector<edges> earr;
bool cmp(edges a, edges b) {
if (a.cost < b.cost) return true;
else return false;
}
bool cmpx(planet a, planet b) {
if (a.x < b.x) return true;
else return false;
}
bool cmpy(planet a, planet b) {
if (a.y < b.y) return true;
else return false;
}
bool cmpz(planet a, planet b) {
if (a.z < b.z) return true;
else return false;
}
int minthree(int n1, int n2, int n3) {
return min(min(n1, n2),n3);
}
void inputs() {
cin >> N;
int tmpx, tmpy, tmpz;
planet tmpp;
for (int i = 0; i < N; i++) { //정점삽입
cin >> tmpx >> tmpy >> tmpz;
tmpp.x = tmpx; tmpp.y = tmpy; tmpp.z = tmpz; tmpp.idx = i;
parr.push_back(tmpp);
rootindex.push_back(i); //처음에 루트는 각자 자기자신
}
}
int find(int r) {
if (rootindex[r] == r) return r;
else { return rootindex[r] = find(rootindex[r]); }
}
void makeedges() { //간선 삽입
edges tmpe;
sort(parr.begin(), parr.end(), cmpx); //x 기준으로 오름차순 정렬
for (int i = 0; i < N-1; i++) {
tmpe.cost = abs(parr[i].x-parr[i + 1].x);
tmpe.index1 = parr[i].idx; tmpe.index2 = parr[i + 1].idx;
earr.push_back(tmpe);
}
sort(parr.begin(), parr.end(), cmpy); //y 기준으로 오름차순 정렬
for (int i = 0; i < N - 1; i++) {
tmpe.cost = abs(parr[i].y-parr[i + 1].y);
tmpe.index1 = parr[i].idx; tmpe.index2 = parr[i + 1].idx;
earr.push_back(tmpe);
}
sort(parr.begin(), parr.end(), cmpz); //z 기준으로 오름차순 정렬
for (int i = 0; i < N - 1; i++) {
tmpe.cost = abs(parr[i].z-parr[i + 1].z);
tmpe.index1 = parr[i].idx; tmpe.index2 = parr[i + 1].idx;
earr.push_back(tmpe);
}
sort(earr.begin(), earr.end(), cmp); //cost기준으로 오름차순 정렬
}
void makeMST() {
int exitcount = 0;
for (int i = 0; i < earr.size(); i++) {
if (exitcount == N - 1) break;
int firstplanet = find(earr[i].index1);
int secondplanet = find(earr[i].index2);
if (firstplanet == secondplanet) continue;
rootindex[secondplanet] = firstplanet;
resultsum += earr[i].cost;
exitcount++;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
inputs();
makeedges();
makeMST();
cout << resultsum;
return 0;
}'알고리즘 문제풀이 > 정렬' 카테고리의 다른 글
| 백준 11652 [C++] (0) | 2021.01.26 |
|---|---|
| 백준 1620 [C++] (0) | 2021.01.09 |
| 백준 10825 [C++] (0) | 2020.10.25 |
| 백준 10814 (0) | 2020.03.02 |
| 백준 1181 (0) | 2020.01.15 |